ボケ防止できず?
前回の班分け検討で、16人4班の4回分け(ダブりなし)を、表を用いてスマートに解決したつもりになっておりました。
まだまだボケてないでしょ!と思っていたのですが、実際に当てはめてみると、3つ目と4つ目に考えた斜め線のクロスでは成り立っていないことに気づきました。ショック。
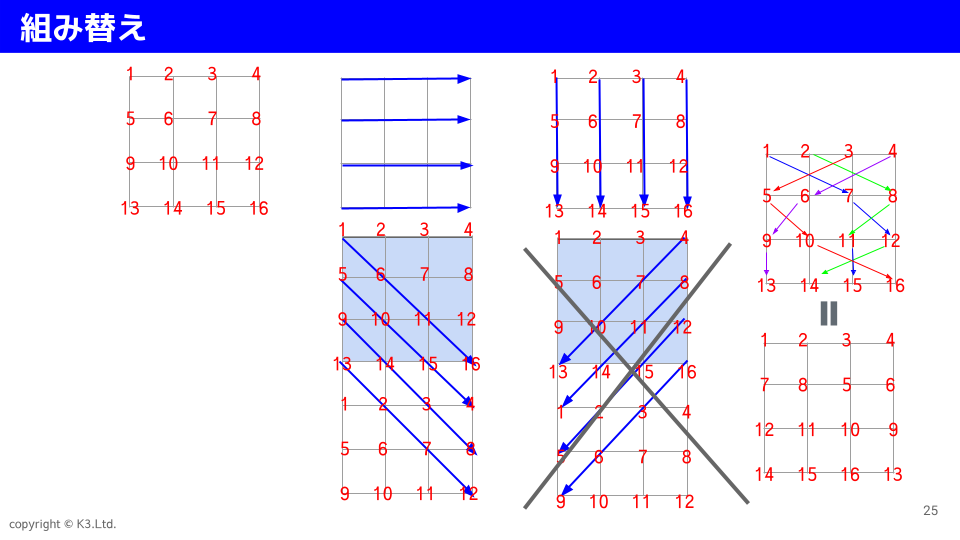
2パターンの斜め線は直交しているので、問題ないと思い込んでいました。
まだ頭の整理がついてないけど、最初(横線)は単なる数字純(+1ごと)、縦線のは4つ飛び(+4)、左側の斜めクロスは実は5つ飛び(+5)に相当。右側は実質3つ飛び(+3)ですね。結果的に5つ飛びと同じ組み合わせが発生してしまいます。
4列なので単純な一律2つ飛びや3つ飛びはダメですな。
図表で解決しようとしていますが、意外と簡単じゃない。
答の1つはなんとなく作れたけど(右端上)、どういうロジックか説明できない。
2行を上下2つずつ反転、3行を反転、4行を1つずらし・・何故?
ボケてはいましたが、結果的にボケ防止に役立つ難題として、頭の体操をさせてくれそうです。